Os fundamentos físico-matemáticos da cosmologia relativista

‘E para nós é o bastante que a gravidade realmente existe (...)’

Princípios Matemáticos da Filosofia Natural, Livro III,
Isaac Newton, 1687

Apresento, abreviadamente, os fundamentos da cosmologia relativista, quais sejam, a Teoria da Relatividade Geral e o Princípio Cosmológico. Discuto alguns modelos relativistas, a saber, o “universo estático de Einstein” e os “universos de Friedmann”. As referências bibliográficas clássicas para as demonstrações tensoriais relevantes são indicadas sempre que necessárias, embora os cálculos em si não sejam apresentados.

1. Introdução

As equações de campo de Einstein da TRG representam uma descrição matemática de uma entidade geométrica, o espaço-tempo, definido por três coordenadas espaciais e uma temporal. Esta entidade de 4 dimensões é estabelecida pelo conteúdo de energia e matéria existentes. Do lado esquerdo das equações temos a descrição geométrica do espaço-tempo e do lado direito, o conteúdo de energia e momento. Colocado de outra forma, a TRG é a teoria da gravitação de Einstein. Ela pode ser entendida simplificadamente pela afirmação de que “o espaço-tempo diz à matéria como se mover e a matéria diz ao espaço-tempo como se curvar” (Taylor e Wheeler 1992, p. 275). Esta é obviamente uma afirmação incompleta pois não só a matéria curva o espaço-tempo mas também toda forma de energia (cf. Harrison 2000, p. 229).

Einstein utiliza o formalismo tensorial para expressar as suas equações de campo, sendo assim, a TRG é uma teoria tensorial. A propósito, o matemático alemão Georg Friedrich Bernhard Riemann (1826-1866) foi um dos principais responsáveis pelo desenvolvimento do cálculo tensorial, tendo importância enorme para a formulação da TRG. Mas, o que é um tensor? Um tensor é uma entidade matemática que possui em cada ponto do espaço n^m componentes, onde n é o número de dimensões do espaço e m é a ordem do tensor. Desta forma, podemos dizer que o escalar é um tensor de ordem 0 — portanto, tem 1 componente — e o vetor é um tensor de ordem 1 — tem n componentes (Harrison 2000, p. 200). Os tensores utilizados na TRG são tensores de ordem m=0,1 e 2 e o “espaço” é o espaço-tempo de n=4 dimensões (três coordenadas espaciais e uma coordenada temporal). Assim, os tensores de segunda ordem da TRG têm, em princípio, 4²=16 componentes. Dizemos “em princípio” porque os problemas físicos reais impõem restrições de simetria que reduzem para 10 as componentes realmente necessárias. Os tensores de primeira ordem são os vetores da TRG, chamados de quadrivetores e possuem 4 componentes.

Faremos uma apresentação simplificada das equações de campo de Einstein que consistem de 10 equações diferenciais não lineares — um sistema de equações. Este sistema se simplifica tremendamente quando são impostas restrições de simetria adicionais dadas pelo PC (ver seção 2 de Hwang 2012) e se reduz a duas equações — somente 2 componentes dos tensores da TRG são necessárias para a formulação completa da cosmologia relativista moderna do Estrondão Quente (tradução de “Hot Big Bang”, cf. Soares 2002).

As equações de Einstein da TRG podem ser expressas de forma qualitativa (Harrison 2000, p. 229) como:

A curvatura do espaço-tempo é dada, matematicamente, pelo tensor de Einstein G_μν:

, (2)

com os índices μ e ν tomando os valores de 0,1,2 e 3. O tensor R_μν é chamado tensor de Ricci, formado a partir do tensor de curvatura de Riemann, o qual é um tensor de ordem 4, sendo a maneira mais geral de se descrever a curvatura de um espaço de n dimensões qualquer. No caso da TRG, o espaço-tempo de 4 dimensões implica na existência de 4⁴=256 componentes. O tensor de Ricci, de ordem 2, é a forma reduzida do tensor de Riemann para ser usada nas equações de Einstein. A forma reduzida é obtida através da aplicação de relações de simetria que eliminam os termos redundantes no tensor de Riemann. O tensor g_μν é o tensor da métrica do espaço-tempo e faz, nas equações de Einstein, o papel do campo (Rindler 2006, p. 179). E é por isto que dizemos “equações de campo de Einstein”. Não falamos, na TRG, em “ação à distância”; um corpo de prova não “sente” diretamente as fontes de matéria e energia, mas sim o campo, i.e., a métrica — a geometria — que estas fontes geram em sua vizinhança. O campo de métrica transmite as perturbações na geometria (ondas gravitacionais) na velocidade da luz, uma situação análoga ao que ocorre no eletromagnetismo (Rindler 2006, p. 179). O campo da métrica é o análogo ao campo gravitacional na teoria newtoniana. Finalmente, o termo R, na Eq. (2), é a curvatura escalar, um escalar associado ao tensor de Ricci e ao tensor da métrica. Em termos tensoriais, a curvatura escalar é igual ao traço do tensor de Ricci com relação ao tensor da métrica. A curvatura escalar é também chamada de escalar de Ricci (Rindler 2006, p. 219).

A parte de matéria e energia das equações de Einstein é dada pelo tensor de energia-momento T_μν. As equações de campo de Einstein completas têm, então, a forma compacta seguinte:

, (3)

onde κ = 8πG/c⁴ é a constante gravitacional de Einstein, G é a constante de gravitação universal e c é a velocidade da luz no vácuo. Finalmente, substituindo a Eq. (2) em (3), temos a forma explícita das 16 equações de Einstein:

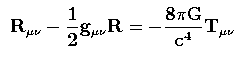
. (4)

E em formato matricial, ainda com as 16 componentes, teremos:

. (5)

Antes de discutirmos as equações de campo de Einstein, apresentadas acima, faremos, na próxima seção, uma descrição do termo que aparece no lado direito das equações 3, 4 e 5, qual seja, o tensor de energia-momento T_μν. Discutimos na seção 3 as equações da TRG, primeiro, as equações para o vácuo, i.e., na ausência de fontes de matéria e energia, e, então, as equações completas, que são as equações relevantes para a cosmologia. Em seguida, passamos às aplicações cosmológicas das equações completas, na seção 4. Aqui, acrescentamos uma novidade, a inclusão da chamada constante cosmológica Λ na Eq. (4), a qual aumenta a sua generalidade. O universo estático de Einstein — onde aparece explicitamente a constante cosmológica — é discutido na seção 4.1 e os universos de Friedmann, nos quais Λ=0, são apresentados na seção 4.2. Na seção 5, apresento algumas considerações finais.

É necessário, neste ponto, fazer uma advertência importante. Não é possível um conhecimento completo e satisfatório da TRG sem o domínio — mesmo que rudimentar — das técnicas do cálculo tensorial. Mas é possível, entretanto, ter-se uma ideia geral do quadro teórico, mesmo sem o aprofundamento nas demonstrações tensoriais. É exatamente isto que pretendo, nesta exposição de uma das mais conhecidas aplicações da TRG, qual seja, a cosmologia moderna. Para o leitor interessado no formalismo matemático tensorial, fornecerei as referências pertinentes sempre que elas forem necessárias.

2. O tensor de energia-momento

As componentes do tensor de energia-momento (Misner, Thorne, Wheeler 1973, p. 137) são as seguintes:

T₀₀ = densidade de matéria e energia.

T_0ν = fluxo de energia (i.e., energia por unidade de área, por unidade de tempo) na direção ν; ν≠0.

T_μ0 = densidade da componente μ do momento; μ≠0.

T_μν = fluxo da componente μ do momento na direção ν (i.e., tensão de cisalhamento). Note que “fluxo do momento” é o mesmo que “força por área”; μ,ν≠0.

T_μμ = fluxo da componente μ do momento na direção μ (i.e., força sobre a área perpendicular, ou seja, pressão, que difere de “tensão de cisalhamento” exatamente por levar em conta a componente da força perpendicular à superfície sobre a qual atua); μ≠0.

O tensor de energia-momento é simétrico, ou seja, T_μν = T_νμ. Misner, Thorne e Wheeler (1973, p. 141) mostram isto utilizando um argumento físico. Eles consideram as tensões de cisalhamento sobre um cubo muito pequeno de aresta L e massa-energia igual a T₀₀L³ e mostram que ele teria aceleração angular infinita caso o tensor não fosse simétrico.

O tensor de energia-momento, por ser simétrico, tem, no máximo, 10 componentes diferentes, ao invés das 16 de um tensor qualquer 4×4. Como veremos a seguir, os tensores relacionados à geometria do espaço-tempo, no lado esquerdo da Eq. (4), também são simétricos.

Estamos prontos agora para discutir, em mais detalhes, as equações de Einstein da TRG.

3. Equações de campo de Einstein

Este foi o caminho seguido por Einstein, e que passaremos a discutir, primeiro, com as equações de campo para a ausência de fontes e, em seguida, com as equações completas, as quais têm como caso particular as primeiras.

Além da redução aos limites newtonianos, Einstein utilizou também, para a postulação das equações de campo, os critérios de simplicidade e de intuição física. Einstein se pergunta: Qual é a forma mais simples da métrica espaço-temporal, na ausência de fontes, que resultará, no limite clássico, na equação de Laplace para o potencial gravitacional newtoniano? E se houverem fontes, como obter da forma mais simples o tensor da métrica e, ao mesmo tempo, a redução clássica à equação de Poisson? E ainda, em ambos os casos da teoria geral, ele deveria obter a conservação da energia e do momento.

Após a satisfação destes critérios e da redução aos limites clássicos, a validade das equações formuladas deve, naturalmente, ser verificada pela experiência. Como veremos, esta verificação ocorreu de forma extremamente satisfatoria para as equações de campo no vácuo, mas, aparentemente, ainda não ocorreu para as equações completas.

3.1. As equações no vácuo

As equações no vácuo são aquelas válidas para o campo da métrica no vácuo, como, por exemplo, o campo em torno do Sol, para o qual a densidade de matéria ρ=0. Estudando as simetrias do tensor de Ricci R_μν no limite clássico do tensor da métrica g_μν (Rindler 2006, p. 222), Einstein postula a seguinte forma, para as equações de campo no vácuo:

R_μν = 0 . (6)

Não são estas, no entanto, as equações de campo que levarão aos modelos modernos da cosmologia relativista. As equações de campo apropriadas necessitam da presença de fontes de matéria e de radiação para serem propriamente aplicadas ao universo. Estas equações de campo, chamadas completas, ainda não tiveram confirmação experimental definitiva (ver discussão em Soares 2009a) e serão apresentadas a seguir.

3.2. As equações completas

As equações de campo de Einstein completas são então escritas como G_μν ≡ R_μν −1/2g_μνR = −κT_μν, onde κ é a constante gravitacional de Einstein, definida na seção 1. Na forma matricial, temos:

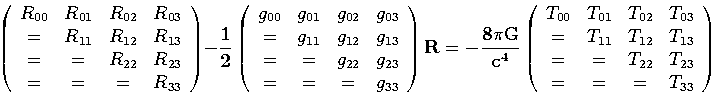
. (7)

É interessante notar que a equação completa reduz-se à equação para o vácuo quando T_μν= 0. Isto ocorre da seguinte forma. A equação completa de Einstein pode ser escrita também na forma R_μν = −κ(T_μν−1/2g_μνT) (Rindler 2006, p. 299). Fica claro, portanto, que para T_μν = 0 teremos R_μν = 0, ou seja, a Eq. (6).

4. Modelos cosmológicos

Rindler (2006, p. 418) mostra como estes cálculos devem ser feitos para uma métrica diagonal genérica dada por:

(ds)² = A(dx₀)² + B(dx₁)² + C(dx₂)² + D(dx₃)² , (8)

Vamos agora obter as equações da cosmologia relativista. O PC, isto é, a redução do universo real a uma idealização homogênea e isotrópica, implica no espaço-tempo com a métrica de Robertson-Walker (Rindler 2006, p. 367), a qual, em coordenadas espaciais esféricas, é dada por:

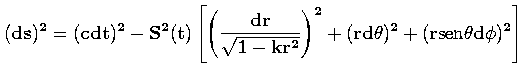
. (9)

S(t) é o fator de escala do universo e k é a constante de curvatura espacial. Esta equação substitui a Eq. (8) para o cálculo do tensor de Einstein aplicado à cosmologia, isto é, ao universo idealizado do PC.

Para aumentar a generalidade das equações de campo, adicionaremos à curvatura escalar uma constante, a chamada constante cosmológica Λ, que será essencial para a discussão do universo estático de Einstein, na próxima seção. Esta constante é chamada cosmológica porque ela só tem relevância no contexto da cosmologia, isto é, para a estrutura e a evolução do universo. A equação de campo completa pode ser escrita então como

R_μν − (1/2R − Λ)g_μν = − κT_μν . (10)

Da mesma forma que a equação completa sem Λ, a equação completa com Λ reduz-se à equação para o vácuo quando T_μν= 0. Como antes, a equação completa de Einstein pode ser escrita também na forma R_μν = −κ(T_μν−1/2g_μνT) + g_μνΛ. Para T_μν = 0 teremos (Rindler 2006, p. 303):

R_μν = g_μνΛ . (11)

Para obtermos as equações da cosmologia relativista faremos a suposição fundamental do PC: toda a matéria — incluindo uma possível “matéria escura” — do universo será, por assim dizer, moída e redistribuída de forma uniforme pelo universo. Teremos desta forma os requisitos físicos do PC, i.e., a homogeneidade e a isotropia da distribuição de matéria. O tensor de energia-momento destas fontes, quais sejam, a matéria e radiação com as características físicas da uniformidade, se reduz aos elementos da diagonal (Rindler 2006, p. 392; Misner, Thorne e Wheeler 1973, p. 140):

T_μν = diag(ρc², −p, −p, −p) , (12)

Devemos notar ainda que p representa a pressão da radiação e da matéria, e, da mesma forma, ρ deve ser dividida numa parte da radiação e numa parte da matéria. A pressão da radiação só será significativa nos estágios iniciais dos modelos em expansão — um gás de fótons a alta temperatura com p = 1/3ρc². A pressão da matéria, a qual só aparece em estágios posteriores, é desprezível. Um fluido perfeito de matéria com pressão nula é muitas vezes chamado, tecnicamente, de poeira. Esta poeira permanece em repouso, no substrato espacial, já que qualquer movimento aleatório constituiria uma pressão. Os movimentos globais de expansão ou contração não são excluídos, no entanto.

O trabalho principal para se obter as equações da cosmologia é aplicar o lado esquerdo das equações de campo dadas pela Eq. (10) — o tensor de Einstein — à métrica de Robertson-Walker dada pela Eq. (9). Já dissemos acima que Rindler (2006, p. 418) mostra os cálculos detalhados para se obter cada elemento do tensor de Einstein. A métrica de Robertson-Walker, sendo a métrica de um universo homogêneo e isotrópico, com as suas inúmeras simetrias, implica em que o tensor de Einstein, com a constante cosmológica, G_μν ≡ R_μν −(1/2R − Λ)g_μν, só terá os elementos da diagonal, exatamente como o tensor de energia-momento:

G_μν = diag(G₀₀, G₁₁, G₂₂, G₃₃) . (13)

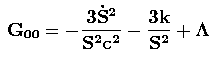
, (14)

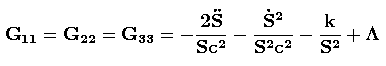
, (15)

onde S é o fator de escala do universo [cf. Eq. (9)].

Com estes valores para G_μν e T_μν, as equações de Einstein completas, G_μν = − 8πG/c⁴ T_μν [Eq. (10)], resultam em apenas duas equações diferenciais não lineares para o fator de escala S(t):

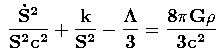
, (16)

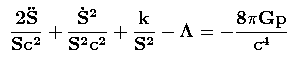
. (17)

As Eqs. (16) e (17) são as equações básicas para a formulação da maioria dos modelos cosmológicos relativistas, com ou sem a constante cosmológica. Além disto, a resolução simultânea deste sistema de equações resulta na equação da conservação da massa e da energia do fluido cósmico (Rindler 2006, p. 393).

A seguir, veremos um modelo cosmológico com Λ e uma família de modelos sem Λ.

4.1. O universo estático de Einstein

4.2. Os universos de Friedmann

O trabalho de Friedmann só foi reconhecido pela comunidade científica muito tempo depois de sua publicação. Em sua homenagem, os modelos resultantes da Eq. (16), sem Λ, receberam o nome de modelos ou universos de Friedmann. Uma discussão detalhada, porém em nível elementar, sobre os modelos de Friedmann está apresentada em Viglioni e Soares (2011).

5. Considerações finais

É importante ressaltar que Friedmann (seção 4.2) obteve originalmente apenas o modelo fechado, por meio das equações completas de Einstein e do PC, o qual foi um conceito cosmológico introduzido por ele. Os três modelos de Friedmann modernos apareceram com a generalização introduzida pela métrica de Robertson-Walker [Eq. (9)], que prevê, ainda, outras topologias espaciais globais, especificadas pela constante de curvatura espacial k, além dos conhecidos modelos abertos hiperbólico, com k=−1, e plano, com k=0 (Rindler 2006, p. 367).

Como foi antecipado em Soares (2009a), vimos, na seção 3.1, que os grandes e decisivos testes da TRG são feitos para uma solução das equações de campo de Einstein no vácuo, isto é, na ausência de fontes de energia e momento. Esta solução tem inúmeras aplicações práticas e é dada pela métrica de Schwarzschild. As soluções mais conhecidas das equações de campo completas são exatamente os modelos da cosmologia relativista, válidas para um fluido homogêneo e isotrópico, e elas falham quando confrontadas com as observações. Os modelos relativistas só sobrevivem quando são postuladas as existências de entidades físicas não observadas, tais como, a matéria escura e a energia escura (cf. Soares 2009a).

Referências

M. Harwit, Astrophysical Concepts (Springer, Nova York, 1998).

E. Harrison, Cosmology – The Science of the Universe (Cambridge University Press, Cambridge, 2000).

F. Hoyle, G. Burbidge, J.V. Narlikar, A Different Approach to Cosmology: from a Static Universe through the Big Bang towards Reality (Cambridge University Press, Cambridge, 2000).

J. Hwang, Modern Cosmology: Assumptions and Limits (arXiv:1206.6297v1 [physics.hist-ph], 2012).

C.W. Misner, K.S. Thorne, J.A. Wheeler, Gravitation (W.H. Freeman and Company, San Francisco, 1973).

W. Rindler, Relativity – Special, General, and Cosmological (Oxford University Press, New York, 2006).

D. Soares, RBEF 34, 1302 (2012), www.sbfisica.org.br/rbef/pdf/341302.pdf.

D. Soares, Uma pedra no caminho da Teoria da Relatividade Geral (www.fisica.ufmg.br/~dsoares/ensino/trg-pdr.pdf, 2009a).

D. Soares, A idade do universo, a constante de Hubble e a expansão acelerada (www.fisica.ufmg.br/~dsoares/ageunv/idadeunv.pdf, 2009b).

D. Soares, A tradução de Big Bang (www.fisica.ufmg.br/~dsoares/aap/bgbg.htm, 2002).

E.F. Taylor, J.A. Wheeler, Spacetime physics introduction to special relativity (W.H. Freeman and Company, New York, 1992).

A. Viglioni e D. Soares, RBEF 33, 4702 (2011), www.sbfisica.org.br/rbef/pdf/334702.pdf.