A floresta encoberta

Proponho um experimento para se verificar o encobrimento de uma floresta “de brinquedo”. O conceito de uma floresta encoberta é muito útil na discussão da questão da escuridão do céu noturno, também conhecida como “paradoxo de Olbers”.

1. Introdução

As árvores representam, portanto, estrelas ou galáxias e a floresta é o universo ou um aglomerado de estrelas. Uma floresta encoberta representa o sistema, de estrelas ou de galáxias, encoberto de luz para o observador em seu interior. As condições para a floresta encoberta são semelhantes às condições para os sistemas cósmicos encobertos.

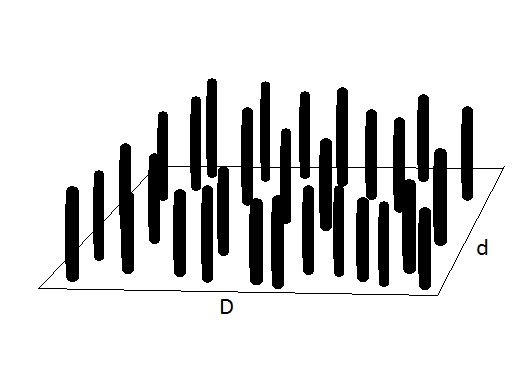
A figura 1 mostra uma floresta de eucaliptos na qual a densidade de árvores e a grossura dos troncos não é suficiente para que a mesma seja encoberta, em outras palavras, para que a visão na direção de visada seja bloqueada por um “muro” de árvores. A grandeza fundamental para a análise do encobrimento é o chamado “limite de fundo” L_F. Se a dimensão da floresta na direção da linha de visada for maior do que L_F, então a visão será encoberta pelo mencionado muro de troncos. Em COSMOS:15mar13 (Soares 2013) mostrei como o limite de fundo pode ser calculado em uma floresta de verdade e sugeri que esta experiência fosse realizada.

Figura 1
Floresta de eucaliptos de uma agroindústria que fotografei ao longo da estrada que liga Pitangui a Martinho Campos na região centro-oeste de Minas Gerais. Na direção da visada o limite de fundo não foi atingido, i.e., a floresta não está encoberta.

Na seção 2 mostro como se calcula o limite de fundo L_F em uma floresta plana bidimensional. Na seção 3 sugiro a construção de duas florestas “de brinquedo” para a verificação experimental da expressão matemática do limite de fundo. Na última seção apresento algumas considerações adicionais.

2. O limite de fundo bidimensional

Mostrarei o cálculo do limite de fundo dado por Harrison (1995) na nota 5 da pág. 267. Há outras maneiras de se chegar ao mesmo resultado, o que pode ser um ótimo exercício de física. Um exemplo será mostrado após a dedução de Harrison.

Considere a “floresta” mostrada na figura 2. A floresta é vista de cima e cada ponto representa o tronco de uma árvore. Suponha que à altura dos olhos todos os troncos apresentam a largura l e cada árvore ocupa uma área igual à área total — ou uma área representativa qualquer — da floresta dividida pelo número de árvores lá existentes. Se o número de árvores na área circular de raio L vale N, então a área média ocupada por uma árvore será A = πL²/N. Note que a densidade de árvores na floresta — o número de árvores por unidade de área — pode ser calculado como n = N/πL², portanto, n = 1/A.

Figura 2
Árvores, representadas pelos pontos, distribuídas aleatoriamente numa floresta. A distância L delimita uma região da floresta que o observador em O vê encobrimento (ou recobrimento) parcial de troncos. A distância para a qual o recobrimento é total é chamada de “limite de fundo” ou “distância de recobrimento”, que também representa o livre caminho médio na floresta.

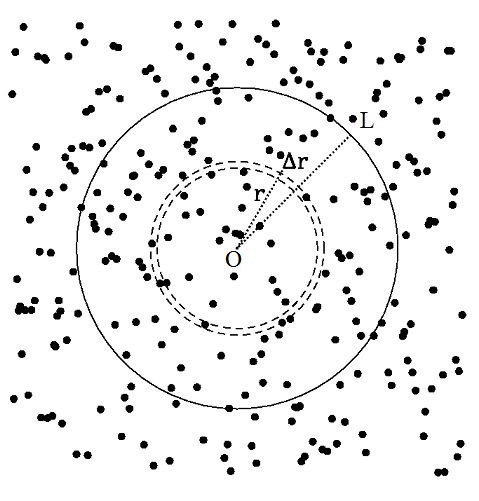A faixa linear recoberta ΔR_recob dentro do anel de largura Δr mostrado na figura 2 será dada pelo número de troncos dentro do anel (n2πrΔr) multiplicado pela largura dos troncos l:

A fração recoberta do anel, que possui comprimento 2πr, será

A fração recoberta até a distância L é obtida somando-se (integrando-se) as contribuições de todos os Δr de O até L:

onde λ = 1/nl é o livre caminho médio na floresta, mencionado acima.

Ora, o recobrimento total da floresta, observado a partir de O, ocorrerá para a fração f = 100%, ou seja,

onde L_F é a distância L para qual f = 100%.

Substituindo a densidade de árvores n por 1/A obtemos a expressão final para o “limite de fundo” ou “distância de recobrimento” L_F, da forma como foi deduzida pelo cosmólogo Edward Harrison:

Uma dedução alternativa é a seguinte. Seja θ o ângulo sob o qual a largura da árvore l, localizada à distância r, apresenta-se ao observador. O valor médio deste ângulo, calculado para as N árvores no interior do círculo de raio L, vale <θ> = l/<r>. O valor médio de r deve ser calculado segundo uma função de distribuição aleatória p(r), que vale p(r) = constante = πL/A [exercício: calcule p(r)]. Obtém-se então <r> = (1/N)∫p(r)rdr = L/2, onde a integral é feita de r = 0 em O até r = L. O valor médio de θ será, portanto, <θ> = 2l/L. O recobrimento ocorrerá quando N × <θ> = 2π, i.e., uma volta completa, e L será o limite de fundo L_F. Teremos N<θ> = N2l/L_F = 2π. Mas N = πL_F²/A, o que resulta em L_F = A/l, como anteriormente.

O limite de fundo será agora utilizado em dois experimentos com florestas “de brinquedo”.

3. Florestas de brinquedo

Figura 3
À esquerda, floresta de brinquedo retangular. À direita, floresta de brinquedo quadrada. Os bastões representam troncos de árvores.

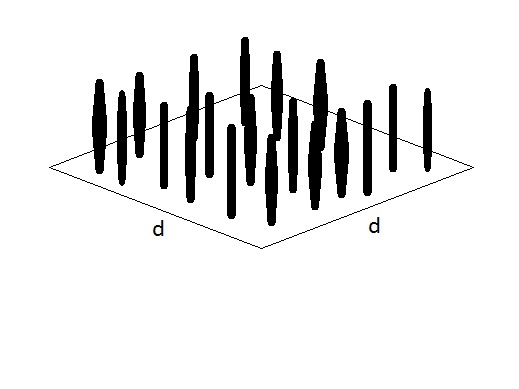
Em cada floresta existem N troncos. O valor de N não pode ser muito pequeno, de forma a garantir a validade das expressões médias utilizadas no cálculo de L_F. É sempre bom lembrar que, grosso modo, a representatividade estatística de uma amostra com N elementos aumenta com N^1/2 [o desvio padrão de uma grandeza é ∝ 1/(N-1)^1/2].

Os troncos podem ser confeccionados serrando-se cabos de vassoura descartados e o “terreno” da floresta pode ser uma placa de papelão duro ou de madeira, sobre o qual os troncos serão colados segundo uma distribuição aleatória.

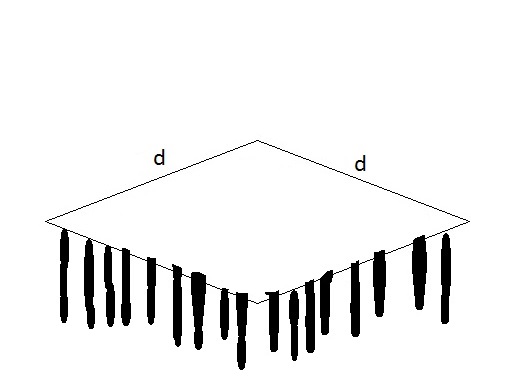
Faremos dois experimentos, um com cada uma das florestas da figura 3.

1) Floresta retangular: distribuir os troncos na área total Dd. Calcular A = Dd/N, e medir l no tronco. Sugere-se medir a circunferência do tronco, em caso de troncos cilíndricos, e calcular l = circunferência/π. Calcular L_F = A/l. O limite de fundo deve ser tal que seja d < L_F < D. A floresta será encoberta segundo a linha de visada ao longo de D, mas não ao longo de d. Ajuste N, D e d para que isto ocorra.

2) Floresta quadrada: faça duas florestas quadradas iguais d×d, de tal forma que elas individualmente não sejam encobertas, ou seja, L_F > d. Superponha agora as duas florestas, fazendo com que uma delas, com os troncos para baixo, interpenetre na outra na vertical, como indicado na figura 4. Desta forma, na floresta composta, o valor de A será reduzido à metade, pois haverá o dobro de troncos na área d² da floresta. O mesmo ocorrerá com L_F, que tornar-se-á menor do que d e a floresta composta resultante será encoberta. Novamente, para que isto ocorra, os valores de N e d deverão ser escolhidos apropriadamente.

Figura 4
Duas florestas de brinquedo quadradas se interpenetram na vertical. A floresta composta resultante será encoberta.

4. Considerações finais

O fato é que há dois pontos fundamentais e uma constatação inevitável, os quais impedem que o céu noturno seja brilhantemente insuportável. Os dois pontos:

1) As fontes de luz não duram para sempre.

2) A velocidade da luz é finita.

E a constatação inevitável: não há energia suficiente, em todo o universo, para que o céu noturno seja mais brilhante do que ele já é.

Como descrito em Soares (2008) e em Harrison (1995), os dois pontos foram apresentados pela primeira vez, surpreendentemente, por um prosador e poeta, o norte-americano Edgar Allan Poe (1809-1849), e a constatação foi claramente explicitada pelo cosmólogo inglês, radicado nos Estados Unidos, Edward Harrison (1919-2007).

Curiosamente, o paradoxo de Olbers não é um paradoxo nem é de Olbers. O inglês William Thomson (1824-1907) — o lorde Kelvin —, um dos mais sagazes estudiosos da questão da escuridão do céu, afirmou em 1887, num discurso acadêmico, que em ciência não existem paradoxos; para ele, os paradoxos eram resultados de mal-entendidos, em outras palavras, do uso equivocado do conhecimento científico, dos fatos experimentais e das evidências observacionais exibidas pela Natureza (cf. Harrison 1995). E a tal questão já era discutida muito antes de o médico e astrônomo alemão Heinrich Olbers (1758-1840) ter chamado a atenção para ela em 1823. O grande astrônomo alemão Johannes Kepler (1571-1630) foi provavelmente o primeiro a propor este problema (Harrison 1995).

A escuridão do céu deve ser bem contextualizada, para evitarmos erros. Se considerarmos outros comprimentos de onda da luz, fora da faixa visível, o céu poderá não ser escuro. Por exemplo, na faixa de micro-ondas há um brilho uniforme em todo o céu, conhecido como “Radiação de Fundo de Micro-ondas” (RFM). Os cientistas partidários da teoria cosmológica padrão consideram-na como um indício atual de um estágio anterior do universo, muito quente; uma explicação alternativa é dada pelo físico canadense P. Marmet (1932-2005), que a atribui ao brilho térmico do meio interestelar (Marmet 2011). Este brilho uniforme de micro-ondas pode ser trivialmente observado: de acordo com um dos descobridores da RFM — o físico Robert Wilson —, 10% do “chiado” que aparece numa tela de TV, ligada a uma antena, fora de sintonia, é devido à RFM; ver seu depoimento no documentário “The Cosmology Quest” (Wilson 2004).

As florestas de brinquedo devem servir de motivação também para as medições de campo. Escolhe-se um bosque, uma mata, mesmo uma floresta, e mede-se A — através da contagem de árvores numa área pré-estabelecida — e mede-se l médio, medindo-se a circunferência de cada tronco nesta mesma área. O valor do limite de fundo L_F pode ser confrontado com a situação real. Se a mata for encoberta, L_F será menor que a sua dimensão na direção da linha de visada.

Agradecimento – A figura 2 foi confeccionada em um dos computadores do Instituto Astronômico Kapteyn, Groningen, Holanda, sob os auspícios do Prof. Reynier Peletier.

Referências

P. Marmet, The 3 K Microwave Background and the Olbers Paradox (www.newtonphysics.on.ca/olbers/index.html, 2011, espólio de P. Marmet).

D. Soares, A escuridão da noite e o universo em que vivemos (www.fisica.ufmg.br/~dsoares/reino/noite.htm, 2008).

D. Soares, COSMOS:15mar13 (www.fisica.ufmg.br/~dsoares/cosmos/13/cosmos5.htm, 2013).

D. Soares, Bosques estelares (www.fisica.ufmg.br/~dsoares/astro/bsqs/bsqs.htm, 2015).

D. Soares, O Reino das Galáxias (www.fisica.ufmg.br/~dsoares/reino/reino.htm, inédito).

R. Wilson, em The Cosmology Quest (youtube.com/watch?v=jOQFLOukrxM, parte 1, youtube.com/watch?v=V4BPxQMUaAM, parte 2, 2004).