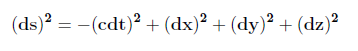
|
, (1) |
26 de dezembro de 2014
A única solução exata da Teoria da Relatividade Geral de reconhecida aplicabilidade prática foi obtida por Karl Schwarzschild em 1916. No limite de campo fraco ela se reduz à lei de gravitação de Newton. Apresento alguns aspectos da gravitação de Schwarzschild e mostro a sua redução à lei de gravitação clássica.
Em janeiro de 1916 o trabalho de Schwarzschild era publicado. Poucas semanas depois, ele encontrou a solução para o interior da massa M. Em maio do mesmo ano, em consequência de doença adquirida na guerra, a brilhante carreira científica de Schwarzschild foi interrompida pela sua morte prematura.
Segundo Rindler (2006, p. 228), a solução externa de Schwarzschild permanece, até hoje, como a mais importante solução exata das equações de campo de Einstein, dada a sua vasta aplicabilidade em sistemas reais. As aplicações mais conhecidas são o cálculo de órbitas planetárias em campos gravitacionais fortes, sendo a previsão correta do avanço anual do periélio de Mercúrio o exemplo mais conhecido, o cálculo do encurvamento da trajetória da luz ao passar nas proximidades de corpos de grande massa, o cálculo do desvio para o vermelho gravitacional, etc. Não se pode deixar de mencionar ainda um grande e novo campo de pesquisa aberto, com a consideração dos objetos denominados buracos negros. Estes surgem como estruturas limites da métrica de Schwarzschild. O buraco negro permanece, no entanto, como uma “hipótese de trabalho”, que aguarda, para sua completa e precisa discussão, a criação de uma teoria de gravitação quântica.
A solução de Schwarzschild das equações gerais da gravitação de Einstein para o espaço exterior a um massa M esférica e estática será daqui para frente denominada gravitação de Schwarzschild em contraposição à gravitação de Newton, a qual é o limite da gravitação de Schwarzschild para grandes distâncias da massa M (a chamada região de campo fraco).
O grande prestígio de que goza a TRG provém fundamentalmente da gravitação de Schwarzschild, que às vezes, de forma equivocada, é confundida com a própria TRG, ou seja, a parte é tomada pelo todo.
Na próxima seção apresento a métrica de Schwarzschild e mostro que ela torna-se a métrica de Minkowski, i.e., a métrica do espaço-tempo plano, da Teoria da Relatividade Restrita (TRR) de Einstein, para distâncias infinitamente grandes da massa M. Na terceira seção, mostro como a gravitação de Schwarzschild se reduz à gravitação clássica de Newton quando as distâncias da massa M são grandes, mas não infinitamente grandes. Apresento na seção 4 algumas considerações finais.
O espaço-tempo da TRR é plano (também chamado euclidiano) e a sua métrica é denominada métrica de Minkowski (ver Soares 2013a). A métrica de Minkowski, em coordenadas cartesianas, caracterizando-o como um espaço plano, é dada pela distância infinitesimal ds entre dois eventos localizados em (t,x,y,z) e (t+dt,x+dx,y+dy,z+dz):
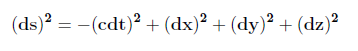
|
, (1) |
onde c é a velocidade da luz no vácuo. Em coordenadas esféricas r, θ e φ ela é escrita como:
|
|
. (2) |
As métricas mostradas nas eqs. 1 e 2 também podem ser escritas em forma matricial e, neste caso, temos os chamados tensores da métrica gμν. Eles são, respectivamente:
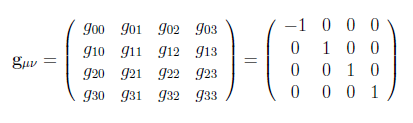
|
(3) |
e
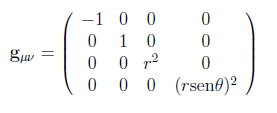
|
. (4) |
Os índices μ e ν tomam os valores 0,1,2 e 3 correspondendo à coordenada temporal e às três coordenadas espaciais. Como pode ser visto nas eqs. 3 e 4, o tensor da métrica de Minkowski só possui os termos da diagonal, o que significa que o tempo e o espaço são isotrópicos (os eixos coordenados são idênticos em qualquer direção) e homogêneos (os eixos são idênticos em qualquer ponto do espaço-tempo). Isto também é verdade para a métrica de Schwarzschild, como mostro a seguir.
A TRR é uma teoria geométrica do espaço-tempo plano (métrica de Minkowski). As métricas da TRG caracterizam espaços-tempos curvos. A métrica de Schwarzschild é a métrica correspondente ao espaço exterior a uma distribuição esférica de massa, sem rotação. O Sol, e muitas outras estrelas e planetas, podem ser aproximados por uma distribuição como esta. A seguir mostrarei como a sua expressão matemática é obtida através da TRG.
A equação principal da TRG é a equação de campo de Einstein, que é uma equação tensorial que envolve tensores 4×4 (o campo aqui é o campo da métrica gμν; ver mais detalhes em Soares 2013b). As equações de campo de Einstein completas totalizam, portanto, 16 (=4×4) equações e são escritas de forma concisa como (Soares 2013b, eq. 4):
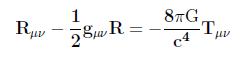
|
, (5) |
onde Rμν é o tensor de Ricci, gμν é tensor da métrica, R é a curvatura escalar e Tμν é o tensor de energia-momento; todas estas grandezas são relacionadas ao sistema a que a equação será aplicada. G é a constante de gravitação universal.
No caso da solução de Schwarzschild Tμν = 0, pois estamos interessados na região externa à distribuição de massa. A equação de Einstein reduz-se às equações de campo para o vácuo Rμν = 0. Rindler (2006, pp. 228-229) calcula os termos da diagonal de gμν para o exterior da distribuição esférica estática, submetida a Rμν = 0. O resultado é a métrica de Schwarzschild. A métrica e o tensor da métrica estão dados abaixo em coordenadas esféricas, as quais são as mais recomendadas devido a simetria do sistema físico correspondente, a saber, uma distribuição esférica de massa. A métrica é:
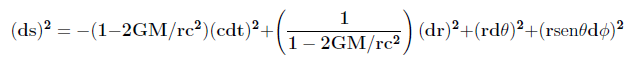
|
(6) |
e o tensor da métrica é:
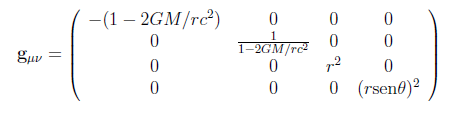
|
. (7) |
As eqs. 6 e 7 representam a métrica de um espaço-tempo curvo, que para distâncias tendendo para o infinito (r → ∞) reduz-se ao espaço-tempo plano de Minkowski da TRR, cuja métrica é dada pelas eqs. 2 e 4, como pode ser facilmente verificado.
“Desde Francis Bacon (1561-1626) acreditava-se que as leis da Natureza estavam aí para serem ‘descobertas’, bastando apenas fazer os experimentos adequados. Einstein nos ensinou uma visão diferente. Ele enfatizou o papel vital da criatividade humana no processo. Newton ‘inventou’ a força da gravidade para explicar o movimento dos planetas. Einstein ‘inventou’ o espaço-tempo curvo e a lei das geodésicas; em sua teoria não há força da gravidade. Se estes dois modelos matemáticos totalmente diferentes podem (quase) descrever as mesmas observações, com certeza deve-se admitir que as teorias físicas não nos dizem o que a natureza é, mas apenas com o que ela se parece. O maravilhoso é que a natureza parece concordar com alguns dos modelos ‘mais simples’ que se podem construir…”A gravitação de Schwarzschild (solução particular da TRG de Einstein) aperfeiçoa a gravitação de Newton e em muitas situações físicas elas fornecem quase as mesmas previsões teóricas para os mesmos fenômenos. Mostrarei neste seção o porquê da palavra “quase” que aparece entre parêntesis no texto de Rindler. Em outras palavras, mostrarei como a gravitação de Schwarzschild — gravitação de espaço-tempo curvo — se reduz à gravitação de Newton — teoria de força da gravidade.
Na seção anterior mencionei que para r → ∞ (ou seja, muito longe da massa M) a métrica de Schwarzschild (eq. 7) se reduz à métrica do espaço-tempo plano (eq. 4), a qual também representa uma região onde não existem massas, ou onde elas são desprezíveis, de tal forma que a gravitação é nula. Para Einstein, esta é uma situação em que o espaço-tempo é plano e para Newton, em que não existe a força da gravidade. Neste caso as duas interpretações são equivalentes.
Agora, antes de r “tender para infinito” tem-se a situação em que r “é grande” mas não “tão grande” como r → ∞. Pergunta-se: como se expressa a métrica de Schwarzschild neste caso? Mostrarei a seguir que existe uma situação em que o espaço-tempo é apenas ligeiramente curvo, que corresponde exatamente à gravitação newtoniana. Para mostrar isto pedirei novamente auxílio ao cosmólogo Wolfgang Rindler (uma demonstração alternativa está em Waner 2002, Lecture 14).
Rindler (2006, p. 188) mostra que a métrica de Schwarzschild pode ser expressa em termos do potencial gravitacional Φ, a linguagem de Newton. A métrica dada pela eq. 6 torna-se:
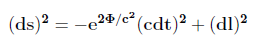
|
, (8) |
em que dl representa toda a parte espacial da métrica (note que para Φ = constante = 0 recupera-se a métrica de Minkowski, eqs 1 e 2). O potencial gravitacional relativista Φ é obtido pela comparação entre as eqs. 6 e 8. Obtém-se (Rindler 2006, p. 230):
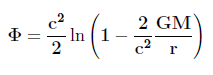
|
. (9) |
A eq. 9 representa a expressão exata do potencial gravitacional relativista equivalente ao espaço-tempo curvo de Schwarzschild. Para distâncias grandes da massa M, o termo 2GM/rc2 é muito pequeno e a função logaritmo pode ser expandida numa série de potências. A expansão logarítmica é dada por:
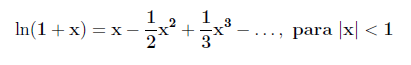
|
. (10) |
Fazendo x ≡ −2GM/rc2, a expansão de Φ é obtida:
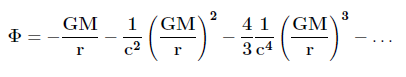
|
(11) |
Tomando-se apenas o primeiro termo da expansão tem-se o potencial gravitacional newtoniano Φ=−GM/r. Em outras palavras, a gravitação newtoniana corresponde a um espaço-tempo ligeiramente curvo, como afirmado anteriormente, pois com esta aproximação o potencial Φ que aparece na métrica mostrada na eq. 8 não é o potencial total. É importante salientar que a expansão logarítmica dada pela eq. 11 só vale para o campo gravitacional fraco; nas vizinhanças da massa M, onde o campo é forte, a equação exata para Φ (eq. 9) deve ser usada.
A métrica de Schwarzschild (eq. 7) pode também ser reduzida a uma forma correspondente à gravitação newtoniana. Para isto é necessário fazer uma nova expansão em série de potências, agora utilizando-se a expansão binomial:
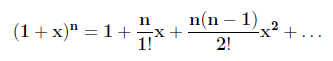
|
. (12) |
O termo (1−2GM/rc2)-1 da eq. 7 pode ser expandido utilizando-se a série de potências acima. Mantendo apenas os dois primeiros termos da expansão temos (1−2GM/rc2)-1 ≅ 1 + 2GM/rc2 e a métrica de Schwarzschild torna-se
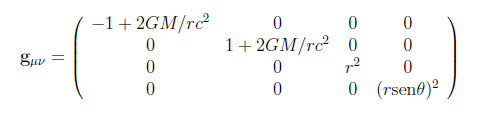
|
, (13) |
que é a métrica ligeiramente curva mencionada, correspondente à gravitação newtoniana. Note que ela é a métrica de Minkowski (eq. 4) com uma perturbação 2GM/rc2. É interessante notar também que se for considerado mais um termo da expansão (eq. 12), a métrica será “quase” newtoniana, o “quase” de que fala Rindler na citação do início desta seção. À medida que mais termos são considerados, a métrica se aproxima cada vez mais da métrica de Schwarzschild. E mais próximo se está da massa M responsável pelo encurvamento do espaço-tempo (e do espaço, cf. Soares 2013a, seção 3.1). A diferença maior entre a gravitação de Newton e a gravitação de Schwarzschild é vista nas regiões de campo gravitacional forte, ou seja, nas proximidades imediatas da massa M. “Campo gravitacional” aqui tem dois significados: para Newton representa a força gravitacional e para Schwarzschild representa a métrica do espaço-tempo.
A solução de Schwarzschild — a gravitação de Schwarzschild — é a única solução da TRG que foi inteiramente comprovada experimentalmente. O seu estrondoso sucesso é muita vezes tomado como sendo o sucesso presumido de todas as possíveis soluções da TRG. Toma-se o sucesso da parte pelo sucesso do todo. E isto não é verdade. Por exemplo, as soluções cosmológicas da TRG, aplicadas ao fluido cósmico (ver Viglioni e Soares 2011, Soares 2012), inclusive o modelo atual da cosmologia, são, sem exceção, soluções não comprovadas experimentalmente até o momento. O modelo da cosmologia moderna só sobrevive às custas de hipóteses importantes ainda não verificadas, quais sejam, as hipóteses das existências da matéria escura não bariônica, da matéria escura bariônica e da energia escura (mais detalhes em Soares 2009).
A TRG é de fato uma teoria ainda incompleta e portanto com aplicação limitada. Uma teoria de gravitação mais completa precisa implementar os preceitos da mecânica quântica em sua estrutura, em outras palavras, ela deve ser uma teoria de gravitação quântica. Ela poderá ter algo da TRG em sua formulação ou poderá ser uma teoria completamente diferente da TRG, assim como a TRG é uma teoria completamente diferente da teoria da gravitação newtoniana.
Este tipo de avanço na ciência não é de forma alguma novo. Ele ocorreu, por exemplo, com a teoria eletromagnética do físico e matemático escocês James Clerk Maxwell (1831-1879). O sucesso do eletromagnetismo de Maxwell é também estrondoso, tem várias aplicações de sucesso, entre elas, a previsão e comprovação experimental de que a luz é uma onda eletromagnética. Mas o eletromagnetismo também encontrou os seus limites, que só foram superados com o advento da mecânica quântica, como foram os casos do efeito fotoelétrico e da radiação do corpo negro.
Em 1948, o físico americano Richard Phillips Feynman (1918-1988) e outros formularam a teoria quântica da eletricidade e do magnetismo, a eletrodinâmica quântica que, com grande sucesso, incorporou a mecânica quântica ao eletromagnetismo clássico. Os interessados encontram uma descrição extraordinária da eletrodinâmica quântica feita pelo próprio Feynman no livreto QED, the strange theory of light and matter (QED é a sigla para “Quantum ElectroDynamics”; Feynman 2006).
O próprio Einstein reconhecia as limitações da TRG, quando aplicada em sistemas físicos que apresentam soluções com singularidades. Os exemplos óbvios estão nos modelos relativistas mais populares da cosmologia moderna, os quais apresentam uma singularidade. Os efeitos quânticos são mais evidentes em situações extremas deste tipo. Singularidades são aberrações teóricas, as quais desaparecem quando uma teoria mais completa é considerada.
W. Rindler, Relativity – Special, General, and Cosmological (Oxford University Press, New York, 2006).
D. Soares, Uma pedra no caminho da Teoria da Relatividade Geral (www.fisica.ufmg.br/~dsoares/ensino/trg-pdr.pdf, 2009).
D. Soares, O universo estático de Einstein (www.sbfisica.org.br/rbef/pdf/341302.pdf, 2012).
D. Soares, Espaço e espaço-tempo nas teorias relativistas (www.fisica.ufmg.br/~dsoares/esptmp/esptmp.htm, 2013a).
D. Soares, Os fundamentos físico-matemáticos da cosmologia relativista (www.sbfisica.org.br/rbef/pdf/353302.pdf, 2013b).
E. Taylor, J.A. Wheeler, Exploring Black Holes: Introduction to General Relativity (Addison Wesley Longman, San Francisco, 2000).
K. Thorne, Black Holes and Time Warps: Einstein's Outrageous Legacy (W.W. Norton & Company, New York, 1994).
A. Viglioni e D. Soares, Observações sobre as soluções clássicas da equação de Friedmann (www.sbfisica.org.br/rbef/pdf/334702.pdf, 2011).
S. Waner, Introduction to Differential Geometry and General Relativity (Lecture Notes) (www.zweigmedia.com/diff_geom/tc.html, 2002).