05 de setembro de 2022

Apresento as funções de energia potencial de dois modelos newtonianos análogos aos modelos cosmológicos de Friedmann. O objetivo da analogia é a discussão didática dos modelos de Friedmann sem e com constante cosmológica.

1. Introdução

Estendo aqui o que foi feito para o modelo estático de Einstein, apresentando modelos newtonianos simplificados para uma discussão dos modelos cosmológicos obtidos pelo matemático e cosmólogo russo Alexander Friedmann (1888-1925), a saber, modelos sem e com constante cosmológica. Entre os últimos, discuto o modelo do Estrondão (cf. Soares 2016). As soluções clássicas de Friedmann estão descritas em Soares (2008) e Viglioni e Soares (2011).

A “constante cosmológica” Λ é um termo de repulsão cosmológica acrescentado por Einstein, em 1917, nas equações de campo originais da TRG, com o objetivo de contrabalançar a atração gravitacional intrínseca do fluido cósmico e assim obter o seu modelo estático de universo (ver mais detalhes sobre Λ, neste contexto, nas seções 1 e 2 de Soares 2012).

A seção 2 é dedicada aos modelos clássicos de Friedmann (Viglioni e Soares 2011), ou seja, modelos sem a constante cosmológica Λ. A seção 3 considera as equações de Friedmann com Λ; aqui, o modelo estático de Einstein e o modelo do Estrondão são as aplicações mais notáveis. Eu termino com alguns comentários adicionais na seção 4.

2. Análogos dos modelos de Friedmann com Λ=0

O análogo newtoniano, em termos de energia potencial do universo, deve conter apenas um termo atrativo de energia gravitacional. A energia potencial do sistema, na posição R, será escrita como:

em que G é a constante universal de atração gravitacional e M é a massa do universo (por convenção, farei G = M = 1). O universo é modelado como uma massa pontual contendo toda a massa e as galáxias são corpos de prova, que se movem no seu campo gravitacional e possuem massa total desprezível em relação a M. Trata-se, portanto, de um modelo bastante simplificado, mas que é útil para algumas análises qualitativas.

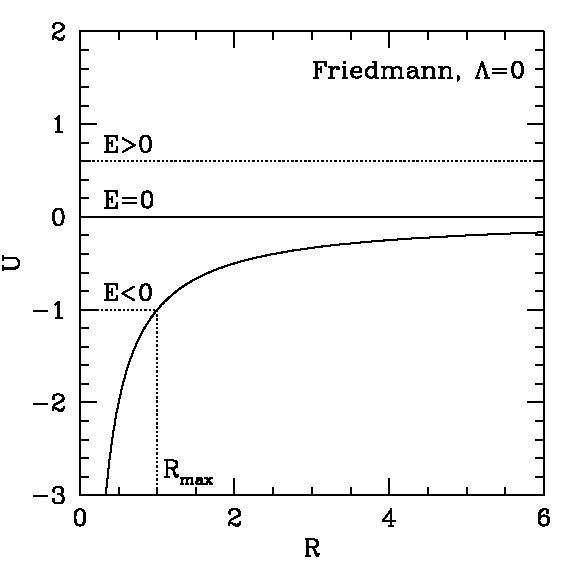
Os universos de Friedmann aberto, plano (ou crítico) e fechado podem ser visualizados neste modelo, conforme a energia total do sistema. Teremos então:

1) universo aberto se a energia total E>0,

2) universo plano se a energia total E=0 e

3) universo fechado se a energia total E<0.

Figura 1
À esquerda, a energia potencial U em função da distância R até a massa geradora do campo gravitacional, sem a constante cosmológica Λ. O fator de escala para os modelos de Friedmann fechado (análogo ao newtoniano com E<0), plano (E=0) e aberto (E>0) estão ao lado (cf. figura 1 de Viglioni e Soares, 2011).

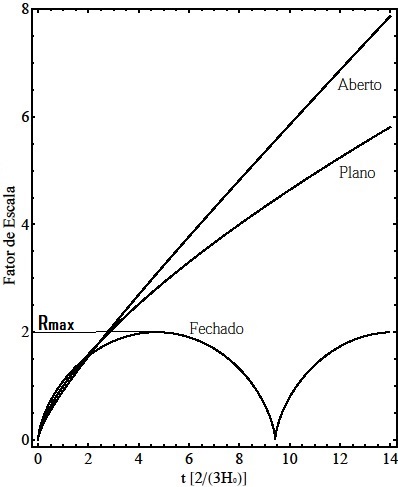
Os modelos aberto e plano representam universos espacialmente infinitos. O modelo plano recebe este nome porque a geometria espacial em grande escala é euclidiana, i.e., obedece aos postulados e teoremas da geometria de Euclides de Alexandria (c. 300 a.C.). O modelo fechado é finito e expande-se até um tamanho máximo, representado, nos dois diagramas da figura 1, por R_max, que é um ponto de retorno pois a partir daí o modelo sofre uma contração. O diagrama de Friedmann para este modelo parece indicar que ele é oscilante, mas isto é apenas aparente e constitui uma extrapolação matemática da solução para a evolução temporal do fator de escala. Este aspecto está discutido mais extensivamente na seção 4. Curiosamente, os modelos oscilantes parecem ganhar força nos últimos anos, mas para obtê-los novos ingredientes deverão ser adicionados aos modelos de Friedmann. As geometrias espaciais e outras características dos modelos clássicos de Friedmann estão discutidas em Soares (2008).

Os modelos aberto e plano possuem expansão desacelerada em toda a sua evolução temporal. O modelo fechado possui uma fase inicial de expansão desacelerada e em seguida uma contração acelerada. Tudo isto pode ser entendido analisando-se a conservação da energia do sistema, que pode ser escrita como:

onde K(R) é a energia cinética do sistema. Vemos que para energia total E ≥ 0, o sistema estará sempre desacelerado, pois, ao se expandir a partir da origem (R = 0), a energia potencial aumentará e, portanto, pela conservação da energia, a energia cinética diminuirá. Para E < 0, o sistema estará desacelerado ao se mover em direção a R_max e estará acelerado ao retornar de R_max.

3. Análogos dos modelos de Friedmann com Λ>0

Repetirei o procedimento adotado em Soares (2012) e escreverei U(R) = U_G(R) + U_Λ(R), onde U_G(R) representa a parte atrativa da energia potencial e U_Λ(R) a parte repulsiva associada à constante cosmológica. Teremos, portanto:

Nesta analogia, a repulsão devida à presença da constante cosmológica está na forma da energia elástica de uma mola, com a diferença importante de ser um termo de energia negativa. A energia potencial elástica da mola usual é do tipo +(1/2)x², ou seja, resulta em uma força de atração para a origem. O termo U_Λ(R) representa uma espécie de energia potencial “elástica” do tecido espaço-temporal, em que o sinal negativo gera uma força repulsiva. Estes dois termos de energia potencial podem ser identificados no lado esquerdo da eq. 4 de Soares (2012), a qual é a equação de Friedmann com constante cosmológica mais um termo de curvatura espacial no lado direito.

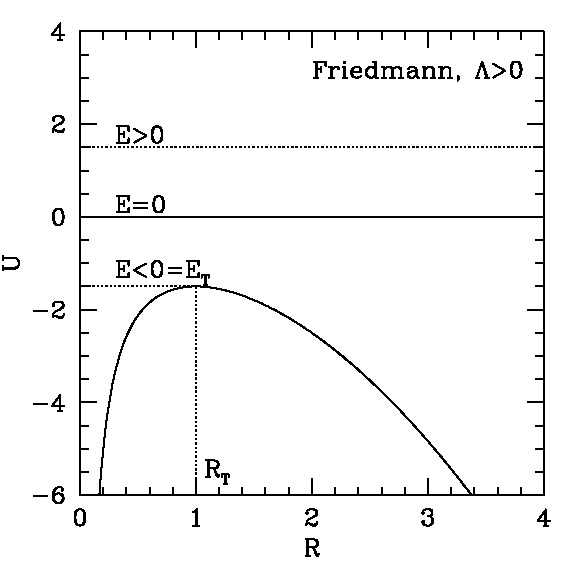
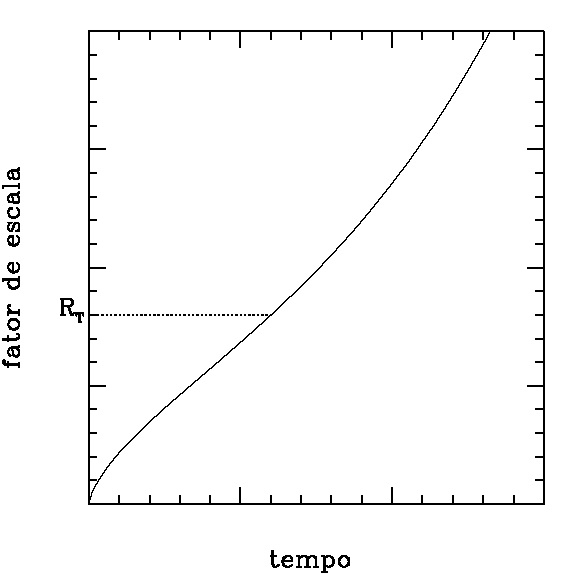
Este análogo newtoniano nos permite visualizar o universo estático de Einstein e o modelo atual do Estrondão com as suas fases de expansão desacelerada e transição para a expansão acelerada. A figura 2 mostra o análogo newtoniano e o diagrama de fator de escala em função do tempo para o modelo atual do Estrondão (cf. Soares 2009 e seção 3.3 de Soares 2015).

Figura 2
À esquerda, a energia potencial U em função da distância R até a massa geradora do campo gravitacional, com constante cosmológica Λ > 0. O fator de escala para o modelo do Estrondão plano, análogo ao newtoniano com E = 0 está ao lado (cf. Soares 2009 e 2015). A distância R_T no diagrama da esquerda representa o raio do universo estático de Einstein (Soares 2012), que ocorre para E < 0 = E_T, ou seja, um sistema ligado ou finito. Este mesmo R_T representa, para um sistema não ligado (e.g., E = 0), um universo que possui uma transição de uma expansão desacelerada (R < R_T) para uma expansão acelerada (R > R_T). A transição entre as duas fases ocorre no fator de escala correspondente R_T, mostrado no diagrama da direita. Note a mudança da concavidade da curva fator de escala × t em R_T.

O análogo newtoniano do universo estático foi apresentado em detalhes em Soares (2012). A parte referente a ele, na figura 2, corresponde à figura 1 de Soares (2012), onde a estabilidade mecânica do modelo é estudada. Podemos ver aqui, na figura 2, que, de fato, o modelo de Einstein é claramente instável, pois ele corresponde a um estado de repouso, o ponto (R_T, E_T), na curva U×R. Uma pequena perturbação no sistema fará com que ele “role” pela crista de energia potencial, seja para o colapso inevitável, seja para a expansão eterna.

Se o sistema possuir energia total E > E_T, por exemplo, E = 0, e vier em expansão a partir da origem, ele realizará uma expansão desacelerada até R_T e acelerada depois de R_T. Senão, vejamos.

Ao se expandir, o sistema “sobe” a crista de energia potencial até R_T e em seguida “despenca” pela crista abaixo. Na subida, a energia potencial U(R) cresce e, portanto, K(R) diminui, mantendo a energia total E constante (cf. figura 2 e conservação da energia). Vemos então que o sistema está desacelerado até R_T. Um raciocínio semelhante mostra que depois de R_T o sistema está acelerado.

4. Considerações finais

Vamos agora a alguns rudimentos de cálculo diferencial e integral para entender melhor a transição expansão desacelerada– expansão acelerada do Estrondão, ilustrada na figura 2, diagrama da direita. Os fundamentos necessários aqui são os conceitos de concavidade de uma curva e ponto de inflexão (e.g., Freire 2015, seção 9.5). R(t), a seguir, representa o fator de escala no eixo vertical da figura 2. O sinal da derivada segunda d²R/dt² indica qual é a concavidade da curva R(t)×t. A figura 2 mostra que a concavidade da curva muda em R = R_T. Este ponto é chamado de ponto de inflexão e nele d²R/dt² = 0. A concavidade da curva é para baixo (d²R/dt² < o, aceleração negativa) antes de R_T, ou seja, o sistema é desacelerado, e é para cima (d²R/dt² > o, aceleração positiva) depois de R_T, ou seja, o sistema é acelerado. É fácil verificar então que os modelos com Λ=0 (figura 1, diagrama da direita) são todos desacelerados, com exceção do modelo fechado depois do ponto de retorno. Mesmo neste caso, a aceleração não muda, apenas o sentido de dR/dt. Em todos os três casos a aceleração d²R/dt² é sempre negativa e as concavidades são todas para baixo e, portanto, são todos desacelerados durante a expansão.

Agradecimento – A figura 1 (U×R) e a figura 2 foram confeccionadas em um dos computadores do Instituto Astronômico Kapteyn, Groningen, Holanda, sob os auspícios do Prof. Reynier Peletier.

Referências

D. Soares, O Big Bang, um “Estrondão” no espaço e no tempo, www.fisica.ufmg.br/dsoares/reino/cosmolg1.htm (2008).

D. Soares, A idade do universo, a constante de Hubble e a expansão acelerada, www.fisica.ufmg.br/dsoares/ageunv/idadeunv.pdf (2009).

D. Soares, O universo estático de Einstein, Revista Brasileira de Ensino de Física, v. 34, n. 1, 1302 (2012).

D. Soares, Universos com constante cosmológica, www.fisica.ufmg.br/dsoares/unilamb/unilamb.htm (2015).

D. Soares, Universo do Estrondão Quente, www.fisica.ufmg.br/dsoares/extn/ueq/ueq.htm (2016).

A. Viglioni, D. Soares, Observações sobre as soluções clássicas da equação de Friedmann, Revista Brasileira de Ensino de Física, v. 33, n. 4, 4702 (2011).

M. Novello, Do Big Bang ao Universo Eterno, www.youtube.com/watch?v=88FG4v885GA (2019).

P. Steinhardt, Bouncing Cosmology, paulsteinhardt.org/bouncing-cosmology (2022).